 Exiten diferentes tipos de derivadas, tales como las usadas en matemáticas, que son las resultantes de un límite que representa a la pendiente de una recta tangente a una gráfica en la función de un punto específico.
Exiten diferentes tipos de derivadas, tales como las usadas en matemáticas, que son las resultantes de un límite que representa a la pendiente de una recta tangente a una gráfica en la función de un punto específico.
La derivada en una función es el límite hacia el que tiende la razón entre un incremento en la función y el que corresponde a la variable si el incremento tiende a ser cero.
Las derivadas de funciones es la que está representada, de forma gráfica, como una línea que es recta pero superpuesta encima de una curva cualquiera que se denomina función. Ese valor que tiene la pendiente respecto al eje en el cual se estudia la función es lo que se denomina derivada.
En lingüística, las palabras derivadas son las que tienen morfemas derivativos. Ejemplo: Bi_ sexual, comid_illa, pajar_illo, etc.
En química, se denomina derivado al producto que se saca de otro por medio de una o varias transformaciones. Como el fuel oil y gas o GLP, la gasolina, que son derivados del petróleo. El término derivado también se aplica a los derivados de la harina, como son pan, galletas, teleras, Bizcochos, etc.
¿Cuáles son los tipos de derivadas y ejemplos?
En lo que se refiere a la clasificación de las derivadas, pueden mencionarse los siguientes tipos:
Derivada de una función
 La derivada de una función f(x) en un punto x=a se define como el valor del límite, cuando existe de un cociente incrementado o incremental, si ese incremento que tiene la variable es similar a cero.
La derivada de una función f(x) en un punto x=a se define como el valor del límite, cuando existe de un cociente incrementado o incremental, si ese incremento que tiene la variable es similar a cero.
Derivada algebraica
En cuanto a los diversos tipos de derivadas en matemáticas, esta consiste en la pendiente de una recta tangente a la función de un determinado punto, por lo que la función tiene que estar en ese punto donde se podrá trazar una recta que es tangente en él.
Derivada del producto
La derivada de un producto en dos funciones es similar al primer factor multiplicado por la derivada del segundo sumándole el segundo factor y multiplicándolo por la derivada del primero. Ejemplo:f(x)=u.v entonces f’(x)=u’.v+u.v’
Derivada del cociente
Entre los diferentes tipos de derivadas, esta se distingue por tiene un cociente en dos funciones es similar a la derivada que tiene el numerador multiplicada por el denominador y menos la derivada que tiene el denominador por el numerador, dividida entre el cuadrado que tiene el denominador. Ejemplo: si f(x)=u/v
Entonces f’(x)=u’.v –u.v’
V 2
Derivadas exponenciales
La derivada de una función que es exponencial es igual a esa misma función por el logaritmo de la base o neperiano multiplicado por la derivada del exponente. Ejemplo: f(x)=au entonces f’(x)=u’.au .Ina
Derivada inmediata
La derivada que tiene una constante siempre es cero
Si f(x)= k entonces su derivada será f’(x)=0
Derivada de suma
Con respecto a qué tipos de derivadas hay, esta se caracteriza por el hecho de que tiene dos funciones es similar a la suma de las demás derivadas que tienen esas funciones. En la derivada de suma esta regla se aplica a números de sumandos tanto positivos como negativos. Ejemplo: f(x)=u ± v entonces
F”(x)=u” ± v
Derivadas de orden superior
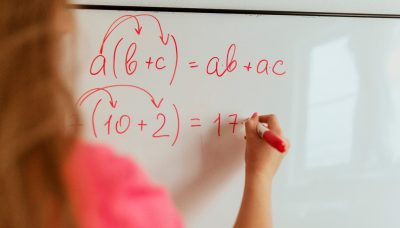 La derivada de cualquier función es derivada de una segunda función cuando si f(X) es una determinada función y tiene una primera derivada f’(x) si la derivada que tiene la función que se ha obtenido, cuando se ha aplicado la derivada, se denomina segunda derivada.
La derivada de cualquier función es derivada de una segunda función cuando si f(X) es una determinada función y tiene una primera derivada f’(x) si la derivada que tiene la función que se ha obtenido, cuando se ha aplicado la derivada, se denomina segunda derivada.
Derivada de la función trigonométrica
Es un proceso en matemática mediante el cual una función trigonométrica cambia con relación a la variable independiente o derivada de una función. Estas funciones de tipo trigonométrico son sin(x), cos(x) y tan(x).
Funciones de derivación implícitas
Es implícita cuando en una función la y son se encuentra despejada y la relación que se da entre x e y está dada por una ecuación de dos tipos de incógnitas en las que el segundo miembro es cero.
Para encontrar la derivación implícita no se necesita despejar y solo tienes que derivar miembro a miembro. Ejemplo: x1=1, entonces y1≠1. Se omite x1 y se deja y1.
Derivadas trigonométricas inversas
Son las funciones inversas a las razones de trigonometría definidas por el seno, coseno y la tangente. Ejemplo: El arcoseno tiende a ser una función inversa del seno.